芝诺：“一个人从A点走到B点，要先走完全部路程的一半，再走完剩下总路程的一半，再走完剩下的一半……”如此循环下去，永远不能到达终点。

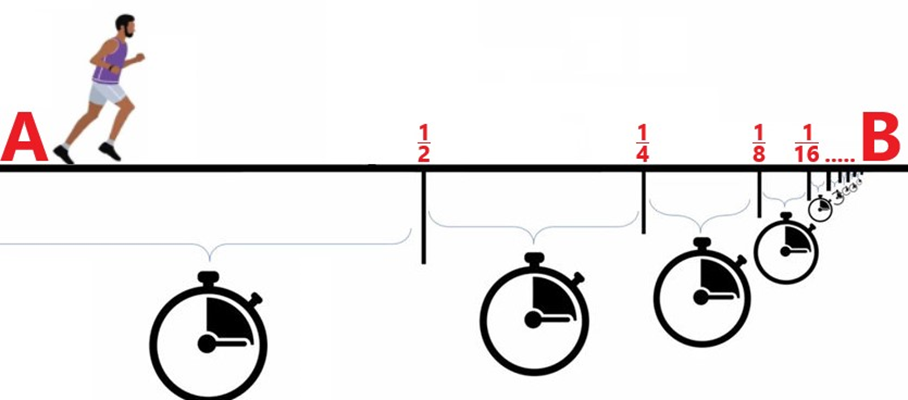
新解：运动者的运动距离及运动距离和为以下2个关联序列，现考察它们在实数域（R）上的有理性：

(1) 运动距离序列

    {a_n=2^-n} = 0  属于 R （1)

(2) 运动路程序列

    {S_n=1-2^-n}=1  属于 R （2)

  从而，在实数集（R）上，这2个序列都为实无穷，是有理可达的。即运动者可以到达极限的目的地。